Matematicas IV (17/02/11)

Identifica  a que tipo de funcion pertenece cada grafica:

Mat IV

https://docs.google.com/document/d/1aaN08zc7aAYmhRWL5_BMWupvJBysciw18DORGJ7_Y7o/edit?hl=en&pli=1#

Erastotenes y la medida de la Tierra. Matematicas II (17/02/11)

Realizar un analisis del documental.

¿si tu estuvieses en lugar de Erastotenes, que otro posible metodo utilizarias?

Fisica II ( 16/02/11)

Si te sumerges en una alberca, en la medida que adquieres una mayor profundidad con respecto a la superficie del agua, mayor fuerza ejerce el agua sobre tu cuerpo, y por lo tanto mayor será la presión que debes soportar. A este tipo de presión debida a la gravedad y la altura se le conoce como presión hidrostática. Para poder determinar la relación exacta entre la presión y la profundidad de un fluido, emplearemos la siguiente ecuación:

                        

                            P = ρgh                          Ecuación 4

En la figura 1.8 se muestra un recipiente para líquidos de forma irregular. Un razonamiento lógico sería considerar que la parte del recipiente con mayor volumen ejercería una mayor presión en el fondo del mismo; sin embargo, las tres secciones (A, B y C) en las que se divide el recipiente tienen el mismo nivel de fluido, por lo tanto, la presión es independiente de la forma o del recipiente. Como se mencionó anteriormente, la presión depende de la fuerza que se aplica sobre una cierta área, en ese sentido, independientemente de que una sección tenga mayor área que otra, la fuerza que aplica la columna de líquido en esa sección es proporcional a su área, lo que provoca que la presión en todo el recipiente sea la misma, porque cada una de ellas se encuentra a la misma distancia vertical por debajo de la superficie. En síntesis, la presión de cada punto con determinado nivel horizontal en un fluido estático es igual. Por lo tanto, la presión al fondo de un recipiente es la misma, independientemente de lo complicada que pueda ser la forma del mismo

1.- Calcular la presión hidrostática en el fondo de una alberca de 5m de profundidad, si la densidad del agua es de 1000kg/m³.

2.-Calcular la profundidad a la que se encuentra sumergido un submarino en el mar, cuando soporta una presión hidrostática de 8x10⁶N/m². La densidad del agua de mar es de 1020kg/m³.

3.-  Determine a que profundidad se encuentra sumergido en un buceador en el mar, si soporta una presión hidrostática de 399 840N/m³.

Existen diversos instrumentos que se utilizan para medir la presión. Uno de los más simples es el barómetro de mercurio (figura 1.9), el cual se emplea para medir el valor real de la presión atmosférica en un lugar determinado. El funcionamiento de este dispositivo es llenando de mercurio un tubo sellado en un extremo e invirtiéndolo, de modo que el extremo abierto esté bajo la superficie de un recipiente que contenga mercurio. Debido a que el tubo está sellado en un extremo, se genera un espacio por encima del mercurio dentro del tubo con una presión igual a cero. La presión del aire produce una fuerza normal que empuja hacia abajo, forzando al mercurio a subir dentro del tubo, el cual se detiene cuando su altura es tal que la fuerza que ejerce hacia abajo es igual a la fuerza hacia arriba que penetra por abajo y sostiene a la columna. Sin embargo, la presión en el fondo de la columna de mercurio es igual a la presión atmosférica. Al medir la altura de la columna mercurio que queda dentro del tubo, se observa que es igual a 760 mm o 29.9 in. Un milímetro de mercurio se denomina como un torr de presión (mm Hg), en honor a Evangelista Torricelli (1608-1647), inventor del barómetro. Por lo tanto, una atmósfera de presión es igual a 760 torr, que equivalen a 1.013 x 105 Pascales.

El manómetro de tubo abierto es otro tipo de medidor de presión común. Es un dispositivo que tiene un tubo en forma de U, con uno de los lados abierto y expuesto a la presión



Matematicas II (16/02/11)

TRIÁNGULOS.

El triángulo es una de las figuras geométricas más utilizadas por los diseñadores de todo tipo de estruc­turas, ya que es la figura plana de mayor resisten­cia a la deformación, por ejemplo en la construcción de puentes o domos geodésicos. Por otra parte, la característica elemental de que tres puntos deter­minan un único plano permite la construcción de asientos de tres patas o los trípodes que sostienen las cámaras fotográficas o de video, entre otros.

Definición y clasificación.

“Un triángulo es una figura plana cerrada con tres lados y tres ángulos”.

Para poder clasificar los triángulos de manera objetiva, en clase efectúen la si­guiente actividad en equipos de trabajo y realicen una exposición de las carac­terísticas y propiedades de los diferentes tipos de triángulos encontrados.

Clasificación de los triángulos.

Por la medida de sus ángulos, los triángulos se clasifican de la siguiente manera.

De acuerdo con la medida de sus ángulos, los triángulos se clasifican como se muestra en la siguiente tabla:

Equilátero:



Tiene tres lados con la misma medida.

Isósceles



Tiene dos lados con la misma medi­da y un lado con medida diferente.

Escaleno



Tiene sus tres lados con diferentes medidas.

Matematicas IV (16/02/11)

2. Según el tipo de expresión que aparece en su forma analítica.

El tipo de expresión que aparece en la regla de correspondencia de una función es lo que le da el nombre. De esta manera, se clasifican en:

Funciones:

Algebraicas: Constante; Identidad; Lineal; Cuadrática; Cubica; Polinomial; Racional; Racional.

Trascendentes: Logarítmicas; Exponenciales; Trigonométricas: Seno, Coseno, Tangente, Cotangente, Cosecante, Secante.

Algunas de estas funciones se abordarán a fondo en las próximas unidades.

Funciones algebraicas:

Una función algebraica es aquélla que puede expresarse en términos de sumas, restas, cocientes, productos y raíces de polinomios.

f (x)= (5x²-2x) / (3+x)

Función constante:

La función constante es de la forma f(x) = c, c es constante; su gráfica es una recta horizontal paralela al eje X separada por una distancia c del eje. Su dominio es todo el eje real; la imagen de todos los argumentos x es. Ejemplo: s(x)=5

Función identidad:

Tiene la forma f(x) = x. Su gráfica es una recta que pasa por el origen formando un ángulo de 45° respecto al eje X. Se puede prolongar en cualquier sentido de manera infinita; el dominio y contradominio de la función es R. Para todo argumento, su imagen es sí mismo.

Función lineal:

Tiene la forma f(x) = mx + b, donde m y b son constantes. Es una recta de pendiente m y ordenada al origen b. El dominio de la función son los valores reales. Ejemplo: f(x) = 5x + 2

Función cuadrática:

Es de la forma f(x) = ax2 + bx + c, a ≠ 0. Es una parábola con eje de simetría vertical. Su dominio son los valores reales.

Función cúbica:

Su expresión analítica es un polinomio de tercer grado de la forma

f(x) = a₀ x3 + bx2 + cx + d, a ≠ 0. La forma de su gráfica depende de los parámetros a, b, c y d.

Función polinomial de grado n:

Este tipo es para casos particulares n = 0, 1, 2…; tiene la forma:

f(x) = a₀xⁿ + a₁x^n–1 + ... + a_n–1x + a_n, a_n ≠ 0, donde a₀, a₁, ... a_n son sus parámetros. Su gráfica depende de los valores de éstos.

El dominio para una función polinomial es R. Acerca de esta función se profundizará más en la unidad 2. Ejemplo: h(x) = 9x⁵ + 5x⁴ + x³ – 2

Función racional:

Está formada por el cociente de dos polinomios, es decir:

 f (x) = p(x)/ q(x) ; con p(x) y q(x) como polinomios y q(x) ≠ 0

El dominio es R, excepto las raíces o ceros del denominador, en donde éste se anula. Esta función se explicará con mayor detalle en la unidad 3.

Función irracional:

Su expresión analítica posee expresiones algebraicas no racionales. Las funciones de este tipo generalmente tienen radicales.

Funciones trascendente:

Entre las funciones trascendentes se encuentran las trigonométricas, logarítmicas y exponenciales. Las funciones trigonométricas las estudiaste con detalle en Matemáticas II, y ahora se abordarán de manera breve. Los dos últimos tipos de función serán motivo de estudio en la unidad IV.

Funciones trigonométricas

La trigonometría es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Las funciones trigonométricas son: seno (sen), coseno (cos), tangente (tan), cosecante (csc), secante (sec) y cotangente (cot).

Identificar la clase a la que pertenecen las siguientes funciones algebraicas.

1. f(x) = –1                                        2. f(x) = 5x⁵ + 9

3. f(x) = 2x² + x – 2                           4. f(x) = 3x

5. g(x) = x ² + 4                                 6. f(x) = (2 – x)^1/2

7. r(x) = (x³ + x) /x

Fisica II (15/02/11)

Presión y sus tipos

La presión (P) es una cantidad escalar, es decir, en cualquier punto tiene magnitud, pero no dirección. El concepto de presión tiene en cuenta la fuerza, así como el área de sección trasversal sobre la que actúa dicha fuerza. La presión P es la magnitud de la fuerza F que actúa perpendicularmente a una superficie, dividida entre el área A de sección trasversal donde la fuerza actúa.

                                 P= F/ A                 Ecuación 3

En el SI la presión se mide en N/m², lo que equivale a un Pascal (Pa). En el Sistema Inglés, la unidad de medida de la presión son las lb/in², o Psi (Pound per Square Inch).

Una persona no podría balancear su peso en la punta de un clavo ya que penetraría su piel. Sin embargo, todos conocemos que es posible acostarse en una cama de clavos debido a que, como lo muestra la ecuación 3, la fuerza F representa el peso de la persona, mientras que el área A es el área de la punta del clavo. Debido a que esta área es muy pequeña, el clavo ejerce una gran presión sobre la persona. Sin embargo, al aumentar el área de contacto y poner muchos clavos, la fuerza se distribuye de forma proporcional, por lo tanto la presión en cada uno de los clavos será muy pequeña.

Un fluido en reposo no produce una fuerza paralela a la superficie que lo contiene ya que en caso de hacerlo fluiría y dejaría de ser estático, debido a que dicha superficie aplicará una fuerza de reacción al fluido, como lo menciona la tercera ley de Newton. De lo contrario, un fluido en reposo ejerce una fuerza perpendicular a las paredes del recipiente que lo contiene.

La fuerza que ejerce un fluido en reposo sobre una superficie es siempre perpendicular a esa superficie debido a que un fluido no posee rigidez. Por lo tanto, un fluido en reposo dentro de un recipiente se encuentra en equilibrio estático bajo las fuerzas perpendiculares de compresión que ejercen las paredes.

Todas las personas nos encontramos bajo el efecto de la atmósfera terrestre, la cual es un fluido que empuja el cuerpo hacia abajo. Este aire que forma la atmósfera es lo suficientemente grande para generar una presión 1.013 x 105 Pa o 14.70 Psi, ambas medidas a nivel del mar. A este valor de la presión se le denomina presión atmosférica y algunos autores le llaman simplemente atmósfera (atm), y resulta ser un valor de suma importancia en el cálculo de los diferentes tipos de presiones que se abordarán en esta unidad. Por lo tanto el valor de esta presión depende de la altura a la que se mida; en este sentido, la presión atmosférica tiende a variar si se mide en una playa o en la cima de una montaña.

Una de las atracciones de la Feria de la ciencia es una cama de clavos en la cual las personas se pueden acostar. Cada clavo tiene una punta con un radio de 1 mm. Si existieran 4 clavos por centímetro cuadrado y la piel de una persona ocupa 0.64 metros cuadrados de forma distribuida en la cama, determina la presión que soporta cada clavo. Considera que la persona tiene un peso de 75 kg.

Solución:

Debido a que el cuerpo se encuentra en equilibrio, la sumatoria de todas las fuerzas en Y debe ser igual a cero. Debemos calcular la magnitud de la fuerza que soportan todos los clavos para el área mencionada, lo que nos permitirá posteriormente calcular la presión en cada uno de ellos.

ΣF_y = 0

                      w = mg = (75 kg)( 9.81 m/s²)= 735.75N

Si consideramos que existen 4 clavos por cm², lo más conveniente es convertir el área para manejar las mismas unidades, por lo tanto 0.64 m² = 6400 cm², que al ser multiplicada por 4, nos muestra que 25 600 clavos soportan a la persona.

Para calcular la fuerza en cada clavo, dividimos el peso de la persona entre el número total de clavos, lo que nos da un valor de 0.0287 N para cada clavo.

El área de cada uno de los clavos, a partir de su radio, se determina de la siguiente manera:

                 A_clavo =∏ r² = ∏(1x 10^-3 m )² =3.14x10^-6 m²

A partir de la ecuación 3, podemos determinar la presión en cada uno de los clavos:

             P = F /A = = 0.0287 N /3.14 x 10^-6 m² = 9.14 x 10³ Pa

Si observas, el resultado anterior refleja que se aplican aproximadamente

25 atm de presión al penetrar la piel.

Resolver los siguientes Problemas:

1.-  Sobre un líquido encerrado en un recipiente se aplica una fuerza de 60N mediante un pistón que tiene un área de 0.01m². ¿Cual es el valor de la presión?

2.- Calcular la fuerza que debe aplicarse sobre un área de 0.3m² para que exista una presión de 420 N/m².

Matematicas IV (15/02/11)

1.2 CLASIFICACIÓN Y TRANSFORMACIÓN DE FUNCIONES.

1.2.1 TIPOS DE FUNCIONES

Para poder estudiar y entender las funciones, existen tres criterios de clasificación: según la de su forma analítica, según el tipo de expresión que aparece en su forma analítica y según la correspondencia entre  sus conjuntos.

1. Según la presentación de su forma analítica

Según este criterio se clasifican en explícitas e implícitas. La función es explícita cuando se presenta despejada la variable dependiente.

La función es implícita cuando en la ecuación que la representa aparecen mezcladas las variables dependiente e independiente.

Expresión Clasificación forma analítica

          y = 9x + 8                                      Función explícita

          y = 4x³ + x² -2                               Función explícita

          x² + 2xy + y² = 5xy²                       Función implícita

          4x – y + 2 = 0                                Función implícita

Para algunos casos es fácil pasar de una forma a otra. Por ejemplo, en su forma implícita, y+ 2x = 5 al pasar a su forma explícita quedaría: y = 5 – 2x, haciendo

 y= g(x), g(x) = 5 – 2x.

La forma analítica que presente una función depende de la naturaleza del problema.

Problemas de Matemáticas IV

Determinar que función es explicita y cual implícita:

1.- x³-3x²+5y=34-23x²

2.- x²+4y=4x

3.- 3x-4=5y-3x²

4.- 9x⁵-23x³=56y-34

Convertir las siguientes funciones implícitas a explicitas:

1.- 4x – y + 2 = 0

2.- 4x³-4y²-7x-9=0

3.- 9y-3x³=45-2x

4.- ax²-bx-cy²= dx+ex²                            

Matematicas II (15/02/11)

Ángulos formados por dos rectas paralelas

Alternos internos:

c y e, d y f

Los ángulos alternos in­ternos son iguales

Alternos externos:

a y g, b y h

Los ángulos alternos ex­ternos son iguales

Colaterales:

a y h, b y g, c y f, d y e

Los ángulos adyacentes, entre paralelas, son suplementarios.

Adyacentes:

a y b, a y d, b y c, c y d



Los ángulos colaterales, entre paralelas, son su­plementarios.

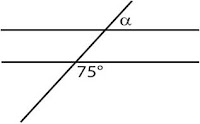
En cada una de las siguientes figuras, calcula los ángulos indicados.

a) Puesto que los ángulos señalados son colaterales, son suplementarios, es decir:

 a + 75 = 180º, de donde, despejando:

 a = 105º                              

b) Los ángulos indicados son alternos externos, por lo tanto, son iguales; es decir:

3x+35 º = 53 º

        3x = 53 º - 35 º                  

        3x = 18 º

X= 6 º                                    

Matemáticas II (14/02/11)

Ángulos formados por dos rectas paralelas y una secante o transversal.
Si observamos las vías de un ferrocarril, tenemos la impresión de que los rieles nunca se cortan, es decir, éstos ilustran la idea de paralelismo.

“Dos rectas son paralelas si no tienen ningún punto en común, es decir, nunca se cortan”.

Una característica de las líneas paralelas es que siempre equidistan, es decir, la distancia entre ellas es siempre la misma. La distancia entre dos rectas paralelas es la longitud de cualquier segmento per­pendicular entre ambas.

Si tenemos dos rectas, ya sean concurrentes o pa­ralelas, decimos que una tercera es secante o trans­versal a ellas si las corta simultáneamente en puntos distintos a cada una de ellas.

Cuando trazamos dos paralelas y las cortamos por una transversal, forma­mos una serie de ángulos cuyas propiedades se emplearán más adelante.

Si trazamos dos líneas paralelas y las cortamos por una secante o transver­sal, formamos una serie de ángulos con características que veremos a con­tinuación.

Los ángulos a, b, g y h están fuera de las paralelas, por lo tanto, se llaman externos. Los ángulos c, d, e, f están entre las paralelas, por lo que son ángulos in­ternos. Los que están sobre las paralelas o bajo las paralelas y del mismo lado de la transversal (b y f, a y e, c y g y d y h); es decir, los que coinciden al colo­carse una recta sobre la otra (b y f, a y e, c y g y d y h), se llaman correspondientes. Los que están dentro de las paralelas y del mismo lado de la transversal, se llaman colaterales. Lo mismo ocurre si están fuera de las paralelas y del mismo lado de la transversal. Si están dentro de las paralelas (uno abajo y otro sobre), pero de lados opues­tos de la transversal, se llama alternos internos. Si están fuera de las paralelas (uno sobre y el otro bajo), pero de lados opuestos de la transversal, se llaman alternos externos. Los que comparten un lado y el mismo vértice, se les cono­ce como adyacentes.



Ángulos formados por dos rectas paralelas

Externos:

a y b, g y h, a y h, b y g

Las parejas de ángulos externos son suplemen­tarios.



Internos:

c y d, e y f, c y f, d y e

Los ángulos internos son suplementarios.



Correspondientes:

a y e, b y f

c y g, d y h

Los ángulos correspon­dientes son iguales.

Opuestos por el vértice:

a y c, b y d , e y g, f y h

Los ángulos opuestos por el vér­tice son iguales.